V.F.Ezhov, M.G.Groshev, T.A.Isaev, V.V.Knjazkov, M.G.Kozlov, G.B.Krygin, N.S.Mosyagin, A.N.Petrov, S.G.Porsev, V.L.Ryabov, A.V.Titov.
Introduction
The story about the study of the weak interaction of elementary
particles demonstrates curious entanglements in modern physics. Weak interactions
grow with energy and, thus, it seems impractical to study them at virtually
zero energy characteristics for atomic physics. The typical scale of weak
interactions in atomic physics is:![]() where
where ![]() is the matrix element of the weak interaction and
is the matrix element of the weak interaction and ![]() is
typical energy interval. Nevertheless, high accuracy of atomic theory and
extremely high sensitivity of atomic experiments made it competitive with
high-energy physics and its high investments. For the first time it was
demonstrated during the study of the parity nonconserving (PNC) weak neutral
electron-nucleon currents, which was found to be in agreement with standard
model (SM) [1]. Since then, there are two trends in the study of the weak
interactions: the continuous growth of the energy and investments in high-energy
physics in order to find new fundamental particles and growth in the accuracy
of both theory and experiment in atomic physics. In present, the sensitivity
of atomic methods is high enough to test SM at the level of radiative corrections.
Atomic physics can also feel the existence of new particles, such as the
second Z-boson, or leptoquark on a TeV scale.
is
typical energy interval. Nevertheless, high accuracy of atomic theory and
extremely high sensitivity of atomic experiments made it competitive with
high-energy physics and its high investments. For the first time it was
demonstrated during the study of the parity nonconserving (PNC) weak neutral
electron-nucleon currents, which was found to be in agreement with standard
model (SM) [1]. Since then, there are two trends in the study of the weak
interactions: the continuous growth of the energy and investments in high-energy
physics in order to find new fundamental particles and growth in the accuracy
of both theory and experiment in atomic physics. In present, the sensitivity
of atomic methods is high enough to test SM at the level of radiative corrections.
Atomic physics can also feel the existence of new particles, such as the
second Z-boson, or leptoquark on a TeV scale.
The experimental search for the permanent electric dipole moments (EDMs) of atoms and molecules provides another powerful tool to for study of even weaker interaction, which violates both parity (P) and time-reversal invariance (T). In SM P- and T-violation is introduces via CM matrix. This mechanism leads to extremely small EDMs of elementary particles, far beyond the reach of modern experimental techniques. However, virtually all extensions of SM predict much larger EDMs. In particular, the super-symmetric models and Left-Right models predict EDMs close to the modern experimental limit [2]. In fact, modern experimental limits on the EDMs of heavy atoms provide the most sensitive tests of these theories.
The search for the P-odd and P,T-odd phenomena in atoms and molecules pushed forward atomic and molecular theory as well as experimental techniques. For the interpretation of the first PNC experiments in atoms the 10% accuracy of the theory was sufficient, but now it is vital to provide a 1% accuracy in order to test SM at the level of radiation corrections.
Here in PNPI, we started to work in this direction in 1981 after detailed discussions in the group of V.M.Lobashev. We were mostly interested in the new possibilities to study P,T-odd interactions in molecules. As a result of those discussions, V.M.Lobashev assigned new experimental group. That group had to start from the very basic level, as the Nuclear Physics Institute had neither equipment nor expertise in molecular beam techniques. It was also an imperative to provide a necessary theoretical background in atomic and molecular calculations to support these experiments.
Parity nonconservation in atoms
There are two main directions in investigation of the PNC effects in atoms. First are the precision measurements of the so-called weak charges QW of heavy nuclei, which generate the dominant nuclear-spin-independent (NSI) term of the PNC atomic amplitudes. These measurements provide a powerful test of SM at low energies. At the 1% level of accuracy it is possible to test the radiative corrections to the theory as well as test various extensions of SM, such as the existence of the second Z boson, or the leptoquark [3].
The second direction of PNC studies is the search of the nuclear-spin-dependent (NSD) PNC effects. These effects are usually two orders of magnitude smaller. For heavy atoms the dominant contribution to NSD amplitudes comes from the P-odd anapole moment of the nucleus. At present there is only one measurement of the anapole moment in Cs [4]. New measurements of anapole moments for other nuclei will give unique information on the PNC forces in hadronic sector.
The NSD PNC effects in light atoms are caused by the NSD weak neutral currents. Corresponding coupling constant k2=l /2(1-4sin2q), where l=1.25, and q is the Weinberg angle. For sin2q@ 0.23, the constant k2 is small and very sensitive to the value of the Weinberg angle. For example, the 1% measurement of this constant would give a 0.1% accuracy for q.
Atomic PNC experiments are not direct: measured PNC amplitudes are proportional to the weak charge and anapole moment of the nucleus, but one needs state-of-the-art atomic calculations to find proportionality coefficients.
The most accurate PNC measurement was made for Cs
[4]. Based on this measurement Bennett and Wieman [5] gave the following
value of the weak charge of 133Cs:![]() ,
while the SM prediction is
,
while the SM prediction is ![]() This
2.3s difference caused numerous theoretical
speculations (see [3]).
This
2.3s difference caused numerous theoretical
speculations (see [3]).
In order to clarify this situation we recalculated the PNC amplitude
in Cs with the particular emphasis on the analysis of the accuracy of the
theory [6]. We found that Breit correction which was not accurately included
in previous calculations shifts atomic result closer to the SM value. We
also analyzed other uncertainties in atomic theory and concluded that the
accuracy of atomic calculation is about 1%. That led to the following value
of the weak charge: ![]() This value is closer to SM prediction and within the error bar there is
no contradiction with SM.
This value is closer to SM prediction and within the error bar there is
no contradiction with SM.
The calculation of PNC amplitude for Cs[6] was a result of a longstanding program for developing new techniques of atomic calculations. Within this program our group made calculations of NSI and NSD PNC amplitudes in Dy [7], Bi [8], and Yb [9]. Calculations of Dy and Yb are used in the ongoing experiments in Berkeley [10,11].
Precision calculations of PNC effects in heavy atoms present a challenge to modern atomic theory. In order to improve the accuracy of these calculations we developed new approach to the calculations of atoms with several valence electrons [12,13]. In this approach we use many-body perturbation theory to form effective operators for valence electrons, which are used to solve few-body valence problem and calculate atomic observables. The theory was tested in a large number of calculations of different atomic properties and proved to be very effective for atoms with 2-3 valence electrons (see [14] and references therein). It was also used to improve the accuracy of calculations of the EDM enhancement factors in diatomic molecules [15,16].
Anapole moment in hyperfine transitions.
Experimental search for the anapole moments of heavy nuclei is going on in several laboratories all over the world. Traditional method is based on the precision measurement of the rotation of the plane of polarization of light by atomic vapor. These experiments are extremely difficult, primarily because the NSD effect is approximately 100 times smaller than the NSI effect. In addition, the hyperfine structure of an optical line is often not completely resolved and the NSD effect manifests itself as a small distortion of the PNC signal profile. Thus, to extract the NSD part of the measured signal, one needs to know the exact profile of the NSI signal, which presents a considerable experimental problem. A different method was suggested in PNPI in 1988 [17]. In this method one will measure the NSD PNC amplitude in a transition between hyperfine components of the ground state of potassium, in which the NSI signal is absent, as was first suggested in [17]. An earlier discussion of the general ideas of the method was given in [18].
There are three main advantages of this experiment in comparison with optical experiments carried out earlier:
First, there is no NSI PNC contribution to the amplitude and the entire PNC signal would be attributed to the NSD part of the PNC Hamiltonian. (The NSI PNC transition amplitude cancels for the case of hyperfine transitions because the NSI interaction causes equal admixtures of opposite parity states to the upper and lower level, which leads to contributions equal in magnitude and opposite in sign to the transition amplitude).
Second, extremely long electron-spin relaxation times (T2 ~ 1s) have been achieved for the ground state hyperfine levels of potassium [19]. This, in turn, makes it possible to achieve extremely high statistical sensitivity to the PNC signal [17].
Third, the method offers very strong suppression of unwanted M1 and Stark-induced transition amplitudes.
These amplitudes typically cause systematic errors in this kind of experiment by masquerading as the PNC amplitude. The main suppressions are as follows. (i) For the isotope 41K in a strong dc magnetic field, the transition wavelength can be as long as 5 meters, corresponding to a frequency of 60MHz (see Fig.1). A cell of size 3 cm can therefore be accurately placed in the node of the magnetic field, thereby suppressing the unwanted magnetic dipole M1 transition amplitude by many orders of magnitude. (ii) The M1 transition matrix element itself is suppressed in a strong applied static magnetic field. In the range 400G – 4 kG, the matrix element varies by an order of magnitude, while both the transition frequency and the PNC amplitude remain essentially unchanged. This, together with (i), permits excellent control of the dominant spurious effects associated with the M1 amplitude (particularly, the most dangerous component having the same signature as the PNC effect under reversals). (iii) The unwanted Stark-induced E1 transition amplitude is suppressed [20] by a factor of at least DEhfs/ (0.1Ry) ~ 10-6 and is negligibly small, here DEhfs is the ground state hyperfine splitting and Ry is the Rydberg constant.
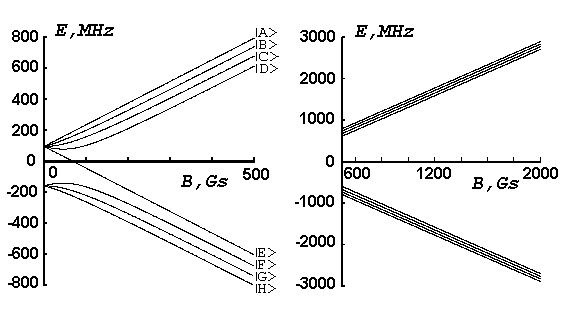
Fig. 1. Energy level diagram for the ground electronic state of 41K as a function of applied dc magnetic field.
In the strong field limit the closest level separation is about one fourth of the initial hyperfine splitting, which is 254 MHz.
The basic idea of the experiment is to measure interference between the allowed M1 and the PNC-induced E1 matrix elements in the transitions between the hyperfine sublevels of the ground state of potassium. The ground state hyperfine energy levels of 41K (state 4s1/2, nuclear spin I = 3/2) are shown in Fig. 1 as a function of magnetic field (the Breit-Rabi diagram). The PNC experiment will involve a series of cycles each involving a laser light pulse for optical pumping, an electric field rf pulse (to drive the PNC E1 amplitude), rf magnetic field pulse (to drive the reference M1 amplitude), a second (probe) laser pulse, and finally, detection of fluorescence light from atoms excited by the probe light pulse.
Optical pumping and probing will be accomplished by circularly polarized diode laser light tuned to the D1 resonance line (l =770nm). As a result of optical pumping by right circularly polarized light (s-), the atoms accumulate in state | E? , the only one decoupled from the light. Once they are in this "dark state", they no longer fluoresce despite the continued presence of the right circularly polarized light. However, when rf electric and magnetic field pulses are applied, tuned to the | E? ®| F? , state | F? is partially replenished. A probe laser pulse immediately after the rf pulses produces resonance fluorescence whose intensity is a measure of the rf transition probability. Alternatively, if one switches the polarization of light from right (s- ) to left (s+), or reverse the direction of the dc magnetic field, one can populate level | A? and look for the | A? ® | B? transition rather than | E? ® | F? . In a high dc magnetic field these two resonances are very close in frequency.
Suppose that the oscillating magnetic field in the rf
pulse is b1=b1cos(w
t)![]() , perpendicular to the dc
magnetic field B0, along the
, perpendicular to the dc
magnetic field B0, along the ![]() axis (see Fig.2 below). This pulse resonantly drives the M1 transition
|
E? ®| F?
(or | A? ®
| B? ) for time tb
such that mb1tb?1,
where m is the transition magnetic dipole moment.
Next, an oscillating electric field e2
along
axis (see Fig.2 below). This pulse resonantly drives the M1 transition
|
E? ®| F?
(or | A? ®
| B? ) for time tb
such that mb1tb?1,
where m is the transition magnetic dipole moment.
Next, an oscillating electric field e2
along ![]() (perpendicular to
both B0 and b1),
is applied for a time te . The electric field
is at the same frequency as b1 and
has a phase offset j :
(perpendicular to
both B0 and b1),
is applied for a time te . The electric field
is at the same frequency as b1 and
has a phase offset j :
e2 =e2cos(w
t+j )![]() .
This electric field drives the PNC-induced E1 transition between the same
two sublevels.
.
This electric field drives the PNC-induced E1 transition between the same
two sublevels.
After these pulses, the amplitude of finding atoms in the state | F? (or | B? ) is:
![]()
![]() (1)
(1)
where
![]() (2)
(2)
d @ 2? 10-14ea0 is the NSD-PNC induced E1 amplitude that was calculated in [17], and the sign of the M1 term is different for transitions | E?® | F? and | A? ®| B? . In these expressions m0 is the Bohr magneton, e is the electron charge, and a0 is the Bohr radius. Following the probe light pulse, one has a fluorescence signal proportional to the population of level | F? :
![]() (3)
(3)
for mb1tb>> de2te. The signal S contains an interference term, which is linear in the desired quantity d. It has a dominant contribution from the anapole moment and a smaller contribution from the AN ?Ve Standard Model coupling, where AN and Ve represent the axial nucleon and the vector electron currents. The interference term can be modulated by chopping the relative phase jof the rf fields between 0 and p and observing the asymmetry:
A = [S(j =0) - S(j =p )]/[S(j =0) + S(j =p )]= 2(de2te)/(mb1tb).(4)
This asymmetry has the signature of the P-odd, T-even invariant b1?B0?e 2. In addition to chopping the relative phase between the rf fields, one thus has another available reversal: change of the polarity of the magnetic field B0 (which has to be accompanied by a flip of circular polarization of light (s-« s+ ). Note also that a flip of circular polarization without reversal of B0 does not change the sign of the PNC asymmetry. (With left circularly polarized light, atoms will be optically pumped to the state | A? (Fig.1), and the rf frequency has to be slightly adjusted, so it is resonant with the | A? ® | B? transition.)
Consider now the main requirements for the experimental setup that follow from the above discussion. (i) One needs a high rf electric field with amplitude e2»1 kV/cm. (ii) A magnetic field B0 »4kG must be applied. (iii) It is necessary to apply both magnetic and electric rf fields. Taking the duration tbof the rf magnetic pulse to be approximately 0.1teand a matrix element of m» 10-2 ea0,, the required amplitude
of the rf magnetic field is b1»10-2G.
An experimental setup satisfying all these requirements is shown schematically in Fig.2. A 64MHz resonator is formed by a l/4coaxial line (1), shorted at one end by an adjustable plunger (2) and closed at the other by a plate not connected to the center conductor. At this end, the electric field e2 is a maximum. A potassium vapor cell (3) is placed in this antinode. A transparent grid across the end of the hollow inner conductor allows fluorescence light to reach detector (6). The resonator is placed between the pole tips of a magnet (5) which provides the field B. For the frequencies of interest the Q-factor of such a resonator can reach 1500. Its resonance frequency can easily be adjusted by changing its length using the plunger (2), without significant change of the field distribution in the cell region. Finally, the resonator screens the cell from the external static and rf fields. One convenient feature of this geometry is that there are no azimuthal currents in the walls of the resonator allowing it to be cut parallel to its axis. The input-coupling loop (7) is inserted through one such cut near the antinode of magnetic field. Other cuts are used to admit the rf magnetic field loop, and the laser beams (4) for optical pumping and probing.
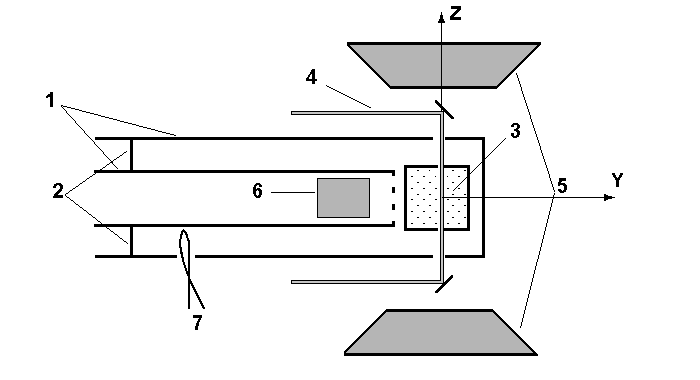
Fig.2. Schematic of the experimental setup for potassium experiment.
This experiment is carried out in collaboration with State Optical Institute.
Parity nonconservation in atomic hydrogen.
Up-to now all PNC experiment were done on heavy atoms, where maximal enhancement is achieved. However, optical experiment with heavy atoms are mostly sensitive to the NSI part of the PNC amplitude. In terms of searching for a new physics the precision measurement of the NSD amplitude is even more interesting. The only NSD amplitude measured by now is the
one in Cs[4], where the dominant contribution to this amplitude comes from the anapole moment of the nucleus (see [1] for the details). Anapole moment is the new PNC nuclear moment, which is of great interest for the nuclear theory, but can not be used to test SM because of the high uncertainty of nuclear calculations.
On the other hand, there is a large enhancement of the NSD P-odd amplitudes of the rf transitions between the hyperfine sublevels of the methastable 2s state of hydrogen. Here the enhancement is caused by the proximity of the level of the opposite parity 2p. The theory here is much more clear and the direct comparison with SM is possible.
The main advantage of the rf experiments in comparison with optical ones is the possibility to separate the antinodes of the rf electric and magnetic fields by means of the resonator design. In order to work with the metastable state one has to use an atomic beam. The main spurious effect in the beam experiments like that is the existence of the motional electric field in the rest frame of an atom, which moves through the dc magnetic field. This motional field mixes levels of opposite parity. In order to reduce this spurious effect one has to reduce the speed of hydrogen atoms and the magnitude of the dc magnetic field.
We have developed the new experimental scheme based on the use of atomic fountain of hydrogen atoms in 2s-state [21]. The crucial fact used to build such a fountain is that the recoil in a two photon transition 1S ® 2S corresponds to the speed 3.2 m/s. That is enough to lift an atom by 0.5 m. To make a fountain we then need a cold atomic cloud at the temperature about 60m K. (That is equivalent to thermal velocities of 1 m/s.)
Let us discuss the possibility of cooling hydrogen to such temperatures. The uniqueness of atomic hydrogen is that is can be excited and heated only by UV light. That allows to use magnetic traps of Ioffe-Prichard type without any additional thermal isolation [22]. That is in contrast with traditional schemes which imply complicated structures inside cryostats with 3He dissolved in liquid 4He. On the first stage hydrogen is cooled to 10 mK collisions with walls, covered with the liquid helium film. Next stage takes place when atoms are evaporatively cooled from the magnetic trap. Because of the final height of the magnetic barrier in such a trap, the velocity distribution is Maxwellian, but with the cutoff from the high-velocity side
We suggest new cooling technique where cooling is caused by the loss of kinetic energy in the process of reflections from the moving magnetic barrier in adiabatically expanding magnetic trap [23]. In fact, this is a magnetic analog of a detander. In this method there is no need in complicated cryogenics and magnetic trap can be non-superconductive. Most important is that cooled gas is easily available for experimenting. Expected cooling rate is determined from the expression for adiabatic expansion:
Tf=Ti(Vi/Vf)2/3exp[k(Si-Sf)].
Here Tf and Vf are final temperature and volume, Ti and Vi are initial temperature and volume and Si and Sfare initial and final entropy. In purely adiabatic process entropy is conserved and cooling is completely determined by the change in volume. Adiabatic conditions are met if the speed of a barrier is smaller than mean thermal speed of a gas. That cab be easily done for temperatures above tens of m K. Below that the evaporative cooling can be used. The advantage of this scheme is that the magnetic trap is on the laboratory bench, not inside the cryostat.
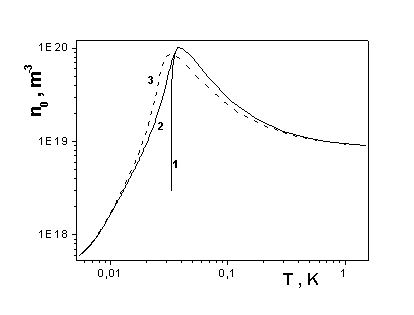
Fig. 3 Different regimes of cooling of atomic hydrogen.
Such source of atomic hydrogen can be used also for the study of the Bose-Einstain condensation and for the frequency standards.
Fig. 3 presents the comparison of evaporative cooling (1), evaporative cooling followed by adiabatic expansion (2), and simultaneous evaporation and cooling (3). In all cases the initial temperature is 1.5K and barrier height is 1Ò. It is seen that at first cooling is mostly determined by evaporation. After the temperature reaches 20-30 mK evaporation is stopped and relaxation losses cause the drop in density.
Experimental setup is shown in Fig. 4. It consists of three blocks, which provide three cooling stages. At first molecular hydrogen is dissociated to produce atomic gas. Then preliminary cooling takes place.
Finally,the adiabatic expansion leads to a further cooling. Magnetic trap is non-superconductive. That allows to change the current in the coils with any necessary speed and significantly simplifies the.
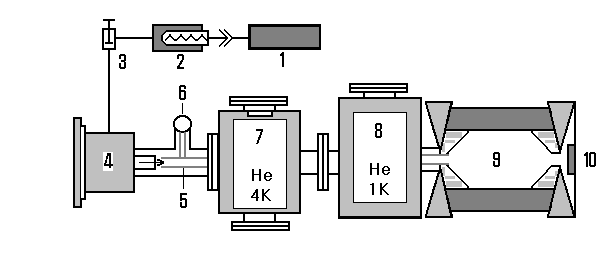
Fig. 4. Schematic of the installation for hydrogen experiment.
1 is the source of molecular hydrogen, 2 is the Pd–filter, 3 is the pulse valve, 4 is a region for rf-dissociation. 5,6 is the teflon tube, cooled to 100 K. 7 is the first helium cryostat and 8 is the second helium cryostat with vapor pumping; 9 is the Ioffe-Prichard trap and 10 is detector.
Calculation of Heavy-Atom Molecules: Generalized RECP Method and Restoration of Electronic Structure in Cores.
Quantum-chemical group of MBL is working upon development of high-precision methods for calculations of heavy-atom molecules. First of all these are the Relativistic Effective Core Potential (RECP) method [24,25], techniques for the electronic structure restoration in heavy-atom cores after the molecular RECP calculation [25], and methods for the generation of the correlation basis sets [26,27]. For very precise calculations of heavy-atom systems we apply the most efficient modern methods of correlation structure calculations and the corresponding codes developed by leading experts. Some improvements in the correlation methods are suggested and applied in our recent calculations on Hg [26], Pb [27], TlH [28] and HgH [29].
Heavy atoms serve as good test systems to assess the accuracy and feasibility of different approximations before they are implemented in more expensive molecular calculations. RECP and all-electron Dirac-Coulomb calculations of energies of transitions between low-lying states of the mercury and lead atoms [26,27] are carried out with the help of two precise methods for the correlation structure calculations. One of them is recently developed mainly by members of our atomic group (see above). It combines the Configuration Interaction (CI) and second-order Many-Body Perturbation Theory (MBPT2 or PT2) approaches. Another one is the Relativistic Coupled Cluster (RCC) method developed by group of Prof. U.Kaldor (Tel Aviv University, Israel). The numerical codes for atomic all-electron four-component calculations, HFD, and for atomic two-component RECP calculations in the jj-coupling scheme, GRECP/HFJ, (developed by Dr. I.Tupitsyn from St.-Petersburg University and by our group) were interfaced with the codes for atomic PT2/CI and RCC calculations.
The results of the RECP calculations are compared with the corresponding all-electron results in order to estimate the accuracy of different RECP versions. It is demonstrated that our version of the RECP method (Generalized RECP or GRECP) [24,25] reproduces the electronic structure in the valence and outer core regions with significantly higher accuracy than other known RECPs, in which the same number of electrons is treated explicitly. We show that at least 34 external electrons of the mercury atom should be correlated and the one-electron basis set should contain up to h-type functions in order to attain a reliable agreement with the experimental data within 200 cm-1.
As is shown in our preliminary analysis, correlations of the 4f electrons with valence and other outer core electrons can be efficiently taken into account at the generation stage of the 20-electron GRECP. The 5s1/2 and 5p1/2,3/2 pseudospinors (electrons) also can be explicitly excluded from GRECP calculations (i.e. “frozen” for the 20-electron GRECP case, see [26]) and their correlations with explicitly treated electrons can be taken with the help of the “correlated” GRECP version providing significant computational savings in precise calculations of molecules containing Hg.
The corresponding RCC calculations on Pb as compared with the CI and PT2/CI calculations are recently finished [27]. Improved scheme of basis set generation and optimization was used in these calculations. The obtained results are comparable by accuracy with those for Hg and conclusions are mainly similar. But essentially 4 electron nature of Pb terms allows us to estimate influence of higher-order cluster amplitudes on correlation structure, and conclude, that such amplitudes should be taken into account in the valence region for high-precision calculations of the properties of the Pb compounds.
Basis set generation.
A new procedure for the generation of basis sets to be used in correlation structure calculations (in which the high speed of the atomic RCC code is efficiently used) was proposed [26,27] and applied to the Hg, Pb, Yb and Tl atoms. The basis sets obtained are employed in our calculations on the Hg and Pb atoms, the HgH, YbF, TlF and PbO molecules and their ions. This procedure allows one to generate equivalent basis sets for RECP (two-component) and for all-electron (four-component) calculations. This is important for comparing the accuracy of different RECPs. The new procedure also makes it possible to control efficiently the quality of the basis sets in the description of correlations in different space regions. In calculations of chemical and spectroscopic properties, the correlations in the outer core region are usually less important than those in the valence region. This allows one to obtain basis sets, which are flexible enough and quite compact at the same time.
GRECP/MRD-CI calculations of Tl and TlH.
The GRECP method was employed in the framework of Multi-Reference single and Double-excitation Configuration Interaction (MRD-CI) method (developed by group of Prof. R.Buenker, University of Wuppertal, Germany) to calculate the spin-orbit splitting in the 2P0 ground state of the Tl atom and spectroscopic constants for the 0+ ground state of TlH. The 21-electron GRECP for Tl was used and the outer core 5s and 5p pseudospinors were frozen with the help of the level shift technique [28]. The spin-orbit selection scheme with respect to relativistic multi-reference states and the corresponding code were developed and applied in the calculations. In this procedure both correlation and spin-orbit interactions are taken into account. A [4,4,4,3,2] basis set is optimized for the Tl atom and employed in the TlH calculations. Very good agreement is found for the equilibrium distance, vibrational frequency, and dissociation energy of the TlH ground state (Re=1.870 ?, ?e=1420 cm-1, De=2.049 eV) as compared with the experimental data (Re=1.872 ?, ?e =1391 cm-1, De =2.06 eV) contrary to other known calculations.
Very recently, good agreement is also found in the GRECP/RCC calculation for the spectroscopic constants of the 0+ ground state in TlH (Re =1.869 ?, ?e =1424 cm-1, De =2.19eV).
GRECP/RCC calculations on the HgH molecule.
GRECP calculations of spectroscopic constants of the HgH molecule ground and low excited states and the HgH+ cation ground state were carried out, with correlation included by the Fock-space RCC method. It is demonstrated that accounting for the basis set superposition errors (BSSE) and connected triple excitations of the 13 outermost electrons are necessary to obtain accurate results for mercury hydride. Spectroscopic constants derived from potential curves which include these terms are in very good agreement with experiment, with errors of a few mbohr in Re, tens of wavenumbers in excitation energies and vibrational frequencies, and proportionately for other properties. Comparison with results of calculations of other groups is also presented. The calculations for excited states are usually the most difficult ones and we present in the table 1 below the results obtained for the 2P1/2 excited state of the HgH molecule.
Table 1.
| Spectroscopic constants for excited 2P1/2 state of the HgH molecule. Re is in ?, Y02 in 10-6 cm-1, other values in cm-1. | |||||||
| Re | we | Te | Be | wexe | ae | -Y02 | |
| Experiment | |||||||
| Ref. [32] | [1.601]a | [1939]a | [6.56]a | [285]a | |||
| Ref. [33] | 1.586 | 2066 | 24578 | 6.68 | [64]a | [0.242]a | |
| Ref. [34] | 1.583 | 2068 | 24590 | 6.70 | 65 | 0.267 | |
| Ref. [35] | 1.583 | 2031 | 24609 | 6.71 | 47 | 0.219 | |
| Present calculations | |||||||
| GRECP/RCC-SD | 1.578 | 2100 | 24044 | 6.75 | 39 | 0.201 | 280 |
| GRECP/RCC-SD(3e-T) | 1.581 | 2080 | 24229 | 6.72 | 40 | 0.205 | 283 |
| GRECP/RCC-SD(13e-T) | 1.582 | 2065 | 24688 | 6.71 | 44 | 0.215 | 286 |
| Other calculations | |||||||
| PP/CASSCF+MRCI+CIPSO [36] | 1.603 | 1946 | 25004 | ||||
| RECP/MRD-CI [37] | 1.615 | 2023 | 25664 | ||||
The GRECP/RASSCF calculations of Ag2 and Ag2+ were also performed [30] to study the applicability of the employed methods to calculations of solids.
Singular operators in atomic cores.
Ab initio calculations [15,16] of the hyperfine, P-odd, and P,T-odd constants for the BaF and YbF molecules are performed with the help of the GRECP/RASSCF/EO scheme recently developed in PNPI. This allows one to take into account correlation and polarization in the outer core region. The electronic wave function of YbF for the ground (2?) state is calculated in the GRECP approximation and the molecular four-component spinors in the core region of ytterbium are restored in the framework of a non-variational procedure. Effects of correlations of core and valence electrons are included with the help of MBPT2 for the Yb atom. For the isotropic hyperfine constant A = (A|| + 2A?)/3, the accuracy of our calculation is about 3% as compared to the experimental datum. The much smaller dipole constant Ad = (A|| - A?)/3 while better than in all previous calculations in the literature, is still underestimated by almost 23 %. A semiempirical correction accounting for the perturbation of the 4f shell in the Yb core due to the bond making, reduces this error to 8%. Our value for the effective electric field on the unpaired electron is 4.9 a.u. = 2.5x1010 Vcm-1.
It is clear from the calculation that the 4f electrons
should be explicitly treated in the planned GRECP/RCC calculation of YbF
with the restoration of molecular four-component spinors in the core of
ytterbium for evaluation of the parameters of P,T-odd spin-rotational
Hamiltonian with high accuracy. Similar calculations for the a(1) excited
state in PbO are in progress now. Besides, GRECP/RCC calculations of the
PNC effects in TlF are in progress now.
Parameters of the spin-rotational Hamiltonian for 171YbF.
| Method | A (MHz) | Ad (MHx) | Wd (1025 Hz/e cm) | WA (Hz) | Ws (kHz) |
| Semiempirical [39] | -1.26 | -43 | |||
| GRECP/SCF [40] | 4932 | 59 | -0.91 | 484 | -33 |
| GRECP/RASSCF [40] | 4854 | 60 | -0.91 | 486 | -33 |
| DHF [41] | 5918 | 35 | -0.31 | 163 | -11 |
| DHF+CP [41] | 7865 | 60 | -0.60 | 310 | -21 |
| Unrestricted DF [42] | -1.203 | -22 | |||
| GRECP/RASSCF/EO | 7842 | 79 | -1.206 | 634 | |
| GRECP/RASSCF/EO
(with 4f-hole correction) |
7839 | 94 | -1.206 | 634 | |
| Experiment [38] | 7617 | 102 |
Molecular EDM experiments
Introduction
The existence of a permanent EDM along the molecular angular momentum explicitly violate P- and T-invariance. Its interaction with the external dc electric field is similar to the Zeeman effect in the dc magnetic field. This interaction results in the change of the magnetic resonance frequency when the direction of either electric or magnetic field is reversed.
Table 2.
| Parameters of the P,T-odd interactions | Atom (experimental accuracy) | Upper limit | TlF | YbF |
| Schff’s moment of the nucleus S | Hg ( <2 10 -9 Hz), [44] | 3 10-50 e cm 3 | 5 10 -5 Hz | |
| g 2 (e-N) | Hg ( <2 10 -9 Hz), [44] | 2 10-8 | 3 10 -5 Hz | |
| g 1 (e-N) | Hg ( <2 10 -9 Hz), [44] | 1 10 –6 | 1 10 -4 Hz | 0.05 Hz |
| Magnetic quadrupole moment of the nucleus M | Cs ( <4 10 -5 Hz), [45] | 1 10-34 e cm 2 | 0.07 Hz | |
| QCD phase ( |
n ( < 10 -7 Hz), [46] | 4 10 –10 | 2 10 -5 Hz | |
| d e EDM of the electron | Tl ( <3 10 -4 Hz), [47] | 5 10-27 e cm | 0.08 Hz |
Polar diatomic molecules have strong internal electric
field ~1011V/cm and they can be easily polarized in a relatively
weak external field. That causes huge enhancement of the P,T-odd
effects and increases sensitivity of the experiment to the EDM of the electron
or the P,T-odd moments of the nucleus. This is illustrated by table
2 [43], where the best experimental results are listed. The first column
shows the source of the P,T-violation. The second column shows the
systems (atoms or neutron), which were used in the experiment and the achieved
limit for a frequency shift. Next column gives corresponding limit for
a P,T-odd parameter in question. The last two columns show corresponding
frequency shifts for diamagnetic molecule TlF and paramagnetic molecule
YbF.
These two molecules are the most convenient for experimental reasons. It
is seen, that physically significant results for TlF molecule correspond
to the frequency shifts about 10-5Hz while for YbF molecule
it is sufficient to measure shifts about 10-2Hz. The accuracy
of the frequency-shift measurements depend on the interaction time ![]() of the molecule with the experimental device.
of the molecule with the experimental device.
Unfortunately, it is impossible to increase this time
by making the experiment in a cell in analogy with neutron or atomic experiments.
The reason is that collisions lead to the change of rotation state and
molecule loose their polarization. Therefore, the time ![]() is equal to the inter-collision time and one has to use molecular beams
where collisions are rare. The accuracy of the beam experiment depend on
the velocity and the intensity of the beam.
is equal to the inter-collision time and one has to use molecular beams
where collisions are rare. The accuracy of the beam experiment depend on
the velocity and the intensity of the beam.
The first molecular beam experiment was done with TlF
in 1969 by the group of P.Sandars [48]. The accuracy for the frequency
shift was only 0.3 Hz. Only after 20 years molecular experiments became
compatible with neutron experiments. In 1989 the group of E.Hinds reached
the accuracy of ![]() Hz [49].
Hz [49].
There are two main obstacles, which limit the accuracy of molecular experiments.
1. There is a spurious effect caused by the quadratic Stark shift, This effect can lead to the frequency shift if in the reversal of the electric field the amplitude of the field changes slightly. For a TlF experiment the change of the amplitude of the field by 0.1 V/cm caused the shift about 10-2Hz (the field was 20kV/cm [49])!
2. A low population of the particular rotational level
in the beam. Molecules have extra degrees of freedom. In particular,
rotational energy is suppressed by the factor me/Mmol
and corresponds to the temperature about 0.1Ê,
while the typical vapor temperature in the molecular source is 1000Ê.
Thus, the population of the ground hyperfine multiplet is only 10-4.
This multiplet includes 12 levels, which brings the population of a level
to ![]() . Thus, to increase
the intensity it is essential that the beam should be cooled.
. Thus, to increase
the intensity it is essential that the beam should be cooled.
We focussed on solving of these problems. As a result, we built the experimental setup for EDM experiment with the TlF molecule. The main features of this setup are:
1) the spurious effect, caused by the quadratic Stark-shift is eliminated by the use of the interference technique [50];
2) differential method is used to increase the reliability of the results and giving control on systematics [51];
3) the beam source with record parameters in terms of the intensity and the population of the ground state is used [52].
Below we describe each of these features in detail.
Interference method
Consider the hyperfine structure of the rotational level
of TlF molecule. In the external magnetic field we have 12 sublevels ![]() ,
which correspond to different projections of the molecular rotational momentum
(J=1) and two nuclear spins (I1=ITl=1/2, I2=IF=1/2).
Previously the following pair of levels was used for the EDM experiment:
,
which correspond to different projections of the molecular rotational momentum
(J=1) and two nuclear spins (I1=ITl=1/2, I2=IF=1/2).
Previously the following pair of levels was used for the EDM experiment:
![]() ,
,
![]() .
.
These levels are not degenerate and the splitting between them depends on the amplitude of the electric field.
On the other hand, there are pairs of levels, which are exactly degenerate in the absence of the magnetic field. These are the so-called Cramers doublets:
![]() and
and ![]() ,
(5)
,
(5)
or
![]() and
and ![]() (6).
(6).
In the magnetic field the degeneracy is reduced, but the splitting does not depend on the electric field. Unfortunately, the rf transitions between these level do not go due to the selection rules and they can not be used for the conventional magnetic resonance.
However, the interference effects between these levels can take place in a zero magnetic field (in optics this is known as Hanle effect) [53]. One has to prepare the beam in a coherent superposition of these states. That can be achieved by the rf transition from a non-degenerate level to the pair of degenerate states.
Suppose that at the entrance to the zero field region
we have a beam of molecules in a state: ![]() ,
where m=
,
where m= ![]() . By inducing
the rf transition
. By inducing
the rf transition
![]()
![]()
we get the coherence mixture of two degenerate states.
In the absence of external fields in the interference region, only the
total phase of the state ![]() .
changes with time. In the presence of the external electric field the degeneracy
is removed only due to the EDM
.
changes with time. In the presence of the external electric field the degeneracy
is removed only due to the EDM ![]() of the Tl nucleus. In this case an extra phase difference between
the states with
of the Tl nucleus. In this case an extra phase difference between
the states with ![]() is equal
to
is equal
to ![]() , where E-is the electric
field and
, where E-is the electric
field and ![]() is the time of
flight through the interaction region
is the time of
flight through the interaction region ![]() with the speed . This phase difference causes the change in population
of the state
with the speed . This phase difference causes the change in population
of the state ![]() after the
inverse transition
after the
inverse transition ![]() .
.
In order to improve the signal to noise ratio we use the
method of the synchronized detection. In this method a weak oscillating
magnetic field ![]() is applied
parallel to the electric field. This leads to an additional time dependent
phase
is applied
parallel to the electric field. This leads to an additional time dependent
phase
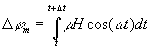
At the end of the interaction region we have a state
![]()
![]()
where ![]() .
If the analyzer is tuned to the transition
.
If the analyzer is tuned to the transition ![]() ,
the probability of the transition will be:
,
the probability of the transition will be:
![]()
where we took into account that ![]() .
The probability W will be periodic function of time with even harmonics
.
The probability W will be periodic function of time with even harmonics ![]() independent on
independent on ![]() and odd
harmonics
and odd
harmonics ![]() proportional
to
proportional
to ![]() . The amplitudes of
these harmonics are proportional to Bessel functions.
. The amplitudes of
these harmonics are proportional to Bessel functions.
By detecting the first harmonics we can measure the phase ![]() ,
while the second harmonics can be used to monitor the beam.
,
while the second harmonics can be used to monitor the beam.
Differential method
Let us note that two pairs of degenerate states (5) and
(6) with projections and ![]() have the EDM of the opposite sign. On the other hand, these states can
be separated in the gradient of the electric field. That can be used to
arrange the differential detection scheme.
have the EDM of the opposite sign. On the other hand, these states can
be separated in the gradient of the electric field. That can be used to
arrange the differential detection scheme.
The polarization rf system at the entrance of the interference region produce two coherent mixtures (5) and (6). After the interference region the beam is splitted by the electrostatic exponential dipole [54] and the phase is analyzed in each beam [55].
The main advantage of this scheme is that the molecules with different signs of the dipole moment pass the interaction region in a same way and at the same time. That allows for a compensation of the spurious effects.
Molecular beam source
The interference method as well as the differential scheme can not be used with the conventional molecular beam sources. These sources have low population of the ground state, large angular spreading and wide velocity distribution. That does not allow to build effective polarization and selection systems. In addition, the interference signal is averaged over the different interaction times. Thus, we need an almost monochromatic slow beam of cold molecules.
In our laboratory a new method of the beam formation has been proposed. It is based on the reduction of the phase space volume by the introducing the vapor of the working substance directly into the expanding supersonic jet of the carrier gas [56]. Due to the collisions with the carrier gas the beam obtains the velocity and the temperature of the supersonic jet. Thermalization is accompanied by the relaxation of the rotational and vibrational degrees of freedom, which causes the increase in the ground state population.
This method allows to separate the formation of the supersonic jet and the production of the high temperature vapor of the working substance [57]. Parameters of the final beam mostly depend on the initial pressure and the temperature of the carrier gas and are limited only by the condensation processes for the carrier during the supersonic expansion [52]. We developed the software and made calculations for the optimization of the beam source parameters [58,59].
Molecular Beam Generator provides the control of main
parameters of molecular beam. It includes the three levels of differential
pump. The speed of pump in the source chamber is equal ![]() l/s
at a vacuum
l/s
at a vacuum ![]() torr.
There is the system of collection, cycling and cleaning of carrier-gas.
The five-coordinate adjustable table provides the automatical adjustment
of the molecular beam source without opening the system to air.
torr.
There is the system of collection, cycling and cleaning of carrier-gas.
The five-coordinate adjustable table provides the automatical adjustment
of the molecular beam source without opening the system to air.
In order to develop this new molecular beam source we had to undertake a detailed study of the physical parameters, which govern the beam formation, the conditions when the condensation takes place, the thermalization processes, etc. For these purposes we built the complex for the experimental diagnostics of the molecular beams
This complex includes the cross-correlation time-of-flight spectrometer, the mass-spectrometer block and selecting quadrupole to study rotational relaxation. This complex was used to find optimal gas-dynamical and geometrical parameters of the beam formation and to measure the beam properties: the velocity distribution, the rotational temperature and intensity [57,60]. It was shown that the main limiting factor for this type of the beam source is the clusterization of the carrier gas.
Note that at present there are no other working installations for the molecular beam study in Russia. Therefore, this complex is of independent importance for such rapidly developing fields as atomic cluster
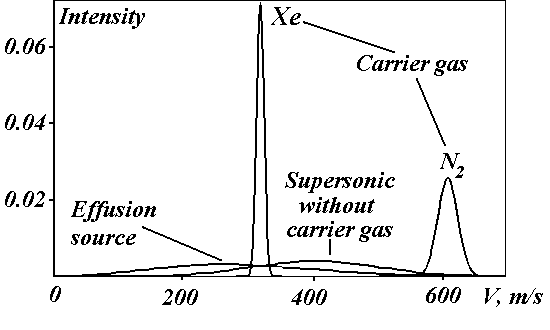
Fig. 4. Relative intensity of the different molecular beam sources
physics. Fig. 4 shows the molecular distributions over the parallel velocity component for a different sources of TlF molecules: the effusive source used in the first EDM experiment [48], the supersonic beam
without carrier gas used by E.Hinds, and our source with two different carrier gases. The use of Xe as a carrier gas allows for more than 4 orders of magnitude increase of the intensity in comparison with the source of E.Hinds [49].
Optimization of molecular beam.
The development of the new beam source with unique parameters required optimization of the installation to reduce the losses of the beam intensity inside the installation. The beam sources with wide velocity distributions did not require accurate calculations of the molecular trajectories inside the working region. In any case only a small part of the velocity distribution was used and any inaccuracy in calculations only meant that in actual experiment the slightly different part of that distribution was used. That did not affect the operation of the installation in a noticeable way. The narrow velocity distribution formed by our source requires very accurate calculations of the trajectories because the beam can miss the detector altogether.
In earlier calculations the quadratic approximation was used for the molecular Stark effect. That resulted in a simple harmonic motion and the analysis was done analytically or even graphically. However, quadratic Stark effect takes place only for a weak field limit, which does not work for a real beam device
We rejected the conventional paraxial approximation for the equations of motion and used numerical solution for the real field configuration. We also used the exact expression for the interaction energy of the molecule with the dc electric field. This approach was combined with the Monte-Carlo method to model the beam inside the spectrometer. As a result, we accounted for all aberrations, including geometrical, chromatic and spherical ones.
That allowed us to make an adequate model of the installation for the EDM measurement for the TlF molecule and to optimize its parameters. During this work we have suggested several original devices for operating the beam. One of them is the electrostatic exponential dipole [54], which is used in the differential scheme described above. Another is the six-electrode double quadrupole lens for the rotational selection and focusing of two close [55]. Depending on the state, the fraction of the initial intensity that reaches the detector is between 1% and 5%.
Conclusion
At present we finished preliminary studies of the beam
source and were able to start the experiment TlF molecule. The statistical
sensitivity of our installation for the EDM precession angle is ![]() Hz.
The TlF experiment is aimed on the measurement of the EDM of the
nucleus. Therefore, this experiment can give information about the P,T-violation
in hadronic sector.
Hz.
The TlF experiment is aimed on the measurement of the EDM of the
nucleus. Therefore, this experiment can give information about the P,T-violation
in hadronic sector.
In order to study the P,T-odd electron-nucleon interactions and supersymmetric theories one needs to measure EDM of the molecule with unpaired electron. These molecules are chemically active radicals and their production and cooling require special investigation, specific for a particular molecule. Beam experiment with such molecules are very complicated; their spin-rotational spectra are not known and should be studied in the preliminary experiments.
At present, the best candidate for such experiments is the YbF [61, 62]. We started these experiments in collaboration with the Sussex University in United Kingdom.
The work in this unconventional for our institute direction was possible due to the comprehensive support from V.M.Lobashev, V.A.Nazarenko and A.P.Serebrov. These studies are part of the State Program in Fundamental Nuclear Physics. We also acknowledge the support by the International Science Foundation and Russian Foundation for Basic Research.
References
[1] I.B.Khiriplovich, Parity nonconservation in atomic phenomena. Gordon and Breach, New-York (1991).
[2] E.Commins. Electric dipole moments of leptons. //In Advances in Atomic, Molecular and Optical Physics. 40, 1 (1999).
[3] D.E.Groom et al, //Review of Particle Physics.,Euro. Phys. J. C, 15, 1 (2000).
[4] C.S.Wood et al //Science, 275, 1759 (1997).
[5] S.C.Bennett and C.E.Wieman //PRL, 82, 2484 (1999).
[6] M.G.Kozlov, S.G.Porsev, and I.I.Tupitsyn //PRL, 86, 3260 (2001).
[7] V.A.Dzuba, V.V.Flambaum, M.G.Kozlov // Phys.Rev. A50, 3812 (1994).
[8] M.G.Kozlov, S.G.Porsev, V.V.Flambaum // J.Phys. B29, 689 (1996).
[9] S G Porsev, Yu G Rakhlina, and M G Kozlov // JETP Lett. 61, 459 (1995); // Hyperfine Interactions, 127, 395 (2000)
[10] A. T. Nguyen, D. Budker, D. DeMille, and M. Zolotorev // PRA 56(5), 3453-63 (1997)
[11] http://phylabs.berkeley.edu/budker
[12] V.A.Dzuba, V.V.Flambaum, M.G.Kozlov //JETP Lett. 63, 882 (1996); PRA 54, 3948 (1996).
[13] V.A.Dzuba, M.G.Kozlov, S.G.Porsev, and V.V.Flambaum // JETP, 87, 885 (1998)
[14] S.G.Porsev, M.G.Kozlov, and Yu.G.Rahlina // JETP Lett., 72, 595 (2000).
[15] M.G.Kozlov, A.V.Titov, N.S.Mosiagin, and P.V.Souchko // PRA, 56, R3326 (1997)
[16] N.S.Mosiagin, M.G.Kozlov, and A.V.Titov // J.Phys.B, 31, L767 (1998).
[17] V.G.Gorshkov, V.F.Ezhov, M.G.Kozlov, and A.I.Mikhailov // Yad.Phys., 48, 1363 (1988).
[18] C.E.Loving and P.G.H.Sandars // J. Phys. B. 14, 2755 (1977).
[19] E.B.Alexandrov, M.V.Balabas, A.S.Pasgalayev et. al. //Laser Physics, 6, 244 (1996).
[20] DeMille D. and Kozlov M. G. //E-print: http://xxx.lanl.gov/abs/physics/9801034
[21] V.F. Ezhov // Preprint PNPI, NP-62-1997, 2205 (1997)
[22] H.F.Hess // PRB, 34, 3476 (1986)
[23] Â.Ô.Åæîâ,Å.Ê.Èçðàèëîâ,Ã.Á.Êðûãèí,Ì.Ì.Íåñòåðîâ,Â.Ë.Ðÿáîâ//ÏðåïðèíòÏÈßÔ 2412(2001)
[24] A.V.Titov, A.O.Mitrushenkov, I.I.Tupitsyn, Chem. Phys. Lett. 185, 330 (1991); N.S.Mosyagin, A.V.Titov, A.V.Tulub, Phys.Rev. A50, 2239 (1994); I.I.Tupitsyn, N.S.Mosyagin, A.V.Titov, J.Chem.Phys. 103, 6548 (1995); A.V.Titov, N.S.Mosyagin, Structural Chemistry 6, 317 (1995).
[25] A.V.Titov and N.S.Mosyagin, Int.J.Quant.Chem., 71, 359-401 (1999)., Rus.J.Phys.Chem. [Zh.Phys.Khimii], 74, Suppl.2, S376-S378 (2000).
[26] N.S.Mosyagin, E.Eliav, A.V.Titov, and U.Kaldor, J.Phys.B, 33(4), 667-676 (2000).
[27] T.A.Isaev, N.S.Mosyagin, A.V.Titov, M.G.Kozlov, E.Eliav, and U. Kaldor, J.Phys.B, 33, 5139-5150 (2000).
[28] Titov A.V., Mosyagin N.S., Alekseyev A.B. and Buenker R.J., Int.J.Quant.Chem., 81(6), 409-421(2001).
[29] Mosyagin N.S., Titov A.V., Eliav E., and Kaldor U. E-print: http://xxx.lanl.gov/abs/physics/0101047.
[30] V.G.Kuznetsov, I.V.Abarenkov, V.A.Batuev, A.V.Titov, I.I.Tupitsyn, and N.S.Mosyagin, Optika i spectroskopiya, 84, 357-363 (1998).
[31] A.V Titov, Int. J. Quant. Chem. 57, 453-463 (1996).
[32] G.Herzberg // Molecular spectra and Molecular structure. I. Spectra of Diatomic Molecules (Van Nostrand Reinhold, New York, 1950).
[33] K.P.Huber and G.Herzberg // Molecular spectra and Molecular structure.IV Constants of Diatomic Molecules (Van Nostrand Reinhold, New York, 1979).
[34] D.Dufajard, B.Majournat and O.Nedelec, Chem.Phys. 128, 537 (1988).
[35] S.Mayama, S.Hiraoka and K.Obi, J.Chem.Phys. 81, 4760 (1984).
[36] U.Haussermann et al., Mol.Phys. 78, 1211 (1993).
[37] A.B.Alekseyev et al., J.Chem.Phys 104, 4672 (1996).
[38] L.B.Knight Jr. and W.Weltner Jr., J.Chem.Phys. 53, 4111 (1970).
[39] M.G Kozlov. J.Phys.B. 30, L607 (1997).
[40] A.V.Titov, N.S.Mosyagin and V.F.Ezhov, Phys.Rev.Lett. 77, 5346-5349 (1996).
[41] H.M.Quiney, H.Skaane and I.P.Grant, J.Phys.B. 31, L85 (1998).
[42] F.A.Parpia, J.Phys.B. 31, 1409 (1998).
[43] M.G.Kozlov, L.N.Labzowsky // J.Phys.B28, 1933 (1995).
[44] J.P.Jacobs, W.M.Klipstein, S.K.Lamoreaux, B.R.Heckel, E.N.Fortson // Phys.Rev. A52, 3521 (1995).
[45] S.K.Peck , D.Krause, L.R.Hunter // (1994) (unpublished).
[46] È.Ñ. Àëòàð¸â, Þ.Â.Áîðèñîâ, À.È.Åãîðîâ, Ñ.Í.Èâàíîâ, Ý.À.Êîëîìåíñêèé, Ì.Ñ.Ëàñàêîâ, Â.Ì.Ëîáàøåâ, Â.À.Íàçàðåíêî, À.Í.Ïèðîæêîâ, À.Ï.Ñåðåáðîâ, Þ.Â.Ñîáîëåâ, Ê.Â.Øóëüãèíà // ßÔ, 59(1), 1 (1996).
[47] E.D.Commins, S.B.Ross, D.DeMille, B.C.Regan // Phys.Rev. A50, 2960 (1994).
[48] G.E.Harrison, P.G.H.Sandars, S.J.Wright // Phys.Rev.Lett. 22, 1263 (1969).
[49] J.D.Cho, K.Sangster, E.A.Hinds // Phys.Rev.Lett. 63, 2559 (1989).
[50] Â.Ô.Åæîâ, Ì.Ã.Êîçëîâ, Â.Ë.Ðÿáîâ, À.Þ.Õàçîâ, Â.Â.ßùóê // Ïèñüìà ÆÒÔ21(15), 34 (1995).
[51] B.N.Ashkinadzi, V.F.Ezhov, M.N.Groshev, V.V.Jaschuk, A.Yu.Khazov, V.A.Knjazkov, M.G.Kozlov, V.L.Rjabov, M.A.Yugaldin // Preprint PNPI 1801(1992).
[52] Á.Í.Àøêèíàäçè, Â.Ô.Åæîâ, Ì.Í.Ãðîøåâ, Â.À.Êíÿçüêîâ, Â.Ë.Ðÿáîâ, À.Þ.Õàçîâ, Â.Â.ßùóê // Ïèñüìà ÆÒÔ20(1), 30 (1994).
[53] Ë.Í.Íîâèêîâ, Ã.Â.Ñêðîöêèé, Ã.È.Ñîëîìàõî //ÓÔÍ 113, 597 (1974).
[54] Â.Ô.Åæîâ, Â.Ë.Ðÿáîâ, Â.Â.ßùóê, À.À.Ìàòûøåâ, Þ.Ê.Ãîëèêîâ, Â.Ë.Âàðåíöîâ // ÆÒÔ 63(5), 117 (1993).
[55] Â.Ô.Åæîâ, Â.Ë.Ðÿáîâ, Þ.Â.Ñîáîëåâ, Â.Â.ßùóê // Ïèñüìà ÆÒÔ21(13), 70 (1995).
[56] Â.Ë.Âàðåíöîâ, Â.Â.ßùóê // Ïèñüìà ÆÒÔ 9(3), 147 (1983).
[57] Â.Ë.Âàðåíöîâ Â.Ô.Åæîâ, Â.À.Êíÿçüêîâ, Â.Ã.Ìóðàòîâ, Â.Ë.Ðÿáîâ, À.Þ.Õàçîâ, Â.Â.ßùóê // ÆÒÔ 57(4), 755 (1987).
[58] Ã.Á.Êðûãèí, Â.Ô.Åæîâ, Â.Ë.Ðÿáîâ, Â.Â.ßùóê // Ïèñüìà â ÆÒÔ, 24(16), 66 (1998) // Ïðåïðèíò ÏÈßÔ 2165 (1997).
[59] Â.À.Êíÿçüêîâ, Í.Ë.Ïîïîâ, Â.Â.ßùóê //Áþë. èçîáð., ò.12, ñ.125 (1993).
[60] Â.Ô.Åæîâ, Â.Â.ßùóê // Ïèñüìà ÆÒÔ 18(9), 1 (1993).
[61] B.E.Sauer, Jun Wang, E.A.Hinds // Phys.Rev.Lett., 74, 1554 (1995).
[62] M.G.Kozlov, V.F.Ezhov // Phys.Rev. A49, 4502 (1994).