![]() , (1)
, (1)
ОРЭПО/РСК-ОД расчет параметров P,T-нечетного взаимодействия в молекуле TlF
.А.Н.Петров, Н.С.Мосягин, Т.А.Исаев, А.В.Титов, В.Ф.Ежов,
E.Eliav, U.Kaldor
В середине пятидесятых годов было обнаружено, что q -мезоны
(распадающиеся на два пиона(p )) и t -мезоны (распадающиеся на три пиона) представляют из себя одну и туже частицу K-мезон. Так как пион и K-мезон являются псевдоскалярными частицами, то стало ясно, что в процессе K(L=0) ® 2p (L=0) пространственная четность (P) не сохраняется. Анализируя распад К-мезонов, Lee и Yang поставили вопрос о несохранении четности в других процессах, и в 1956 г. Wu и др. экспериментально обнаружили, что при b -распаде радиоактивного ядра вероятность испускания электронов с правой поляризацией оказывается меньшей чем для электронов с левой поляризацией.В 1974 году было завершено создание единой теории электрослабого взаимодействия, которая единым образом описала электромагнитные, сохраняющие четность, и слабые, не сохраняющие пространственную четность взаимодействия. К настоящему моменту P-нечетные эффекты обнаружены во всех процессах, обусловленных слабым взаимодействием.
Однако такие объекты, как атомы, молекулы и кристаллы являются с высокой степенью зеркально симметричными, поскольку в них P-четное электромагнитное взаимодействие значительно превосходит P-нечетное слабое взаимодействие электронов с нуклоном. В 1974 г. Bouchiat показал, что P-нечетные электрон-нуклонные взаимодействия значительно усиливаются в тяжелых атомах и молекулах из-за большой электронной плотности на ядре. Усиление этих эффектов также происходит при наличии близко расположенных уровней противоположной четности.
Впервые эффект несохранения четности в атомах был обнаружен в 1978 г. в Новосибирском Институте Ядерной Физики. Было открыто, что пары атомарного висмута вращают плоскость поляризации лазерного луча.
В отличие от P-нечетных процессов, экспериментально подтвержденной теории, описывающей неинвариантные относительно обращения времени (T-нечетные) процессы, в настоящий момент не существует. Единственным известным T-нечетным процессом является распад долгоживущего K
0-мезона, обладающего отрицательной CP четностью (C-операция зарядового сопряжения), на два p -мезона – систему, обладающую положительной CP-четностью. В силу CPT теоремы, это означает неинвариантность данного процесса по отношению к обращению времени.Принципиальным для теории T-нечетных процессов является поиск электрического дипольного момента (ЭДМ) элементарных частиц, таких как электрон, нейтрон или протон. Такой (Р,Т-нечетный) ЭДМ должен быть направлен по спину (
S) этих частиц. Член в гамильтониане (~S× E), соответствующий взаимодействию ЭДМ с внутренним электрическим полем (E), является T-нечетным, поскольку псевдовектор S меняет знак при обращении времени, а вектор E не меняет. Это взаимодействие является также P-нечетным, так как псевдовектор S – P-четный, а E – P-нечетный вектор.В настоящей работе рассмотрено взаимодействие ЭДМ протона в молекуле TlF. Данная молекула, вследствие простой структуры ядра атома таллия (один неспаренный протон), сильного внутреннего электрического поля, близости вращательных уровней и других особенностей, является
одним из наиболее удачных объектов экспериментов, направленных на измерение ЭДМ протона [1].В 1963 году
Schiff [2] показал, что для нерелятивистской квантовой системы частиц с одинаковым пространственным распределением электрического заряда и дипольного момента в произвольном внешнем электрическом поле, взаимодействие дипольного момента с внутренним и внешним электрическим полем в первом порядке по дипольному моменту не дает вклада в энергию системы. В случае взаимодействия c ЭДМ протона теорема остается в силе и при учете релятивистских эффектов в движении электрона. В силу малости дипольного момента протона эффекты второго порядка оказываются пренебрежимо малыми. Учет конечного размера ядра, благодаря которому распределение заряда и дипольного момента по ядру оказывается различным (“объемный” эффект), и магнитное взаимодействие электронов с магнитным моментом и ЭДМ нуклонов (“магнитный” эффект), приводит к ненулевой энергии взаимодействия ЭДМ.Hinds и Sandars [
3], представили взаимодействие ЭДМ протона в молекуле TlF через эффективный гамильтониан вида:![]() , (1)
, (1)
где
![]() , (2)
, (2)
где
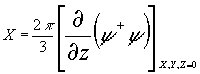 , (3)
, (3)
где
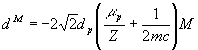 , (4)
, (4)
где
![]() . (5)
. (5)
Параметры
Цель настоящей работы – расчет параметров
Расчет проводится методом Обобщенного Релятивистского Эффективного Потенциала Остова (Обобщенный РЭПО или ОРЭПО)
[4] с последующим восстановлением правильного поведения спиноров в области ядра атома таллия [5]. Для учета электронной корреляции использован наиболее перспективный из современных корреляционных методов – Релятивистские Связанные Кластеры (РСК) с однократными и двукратными кластерными амплитудами. Описание метода расчета представлено в следующей главе.Расчет волновой функции основного (X0
+) состояния молекулы TlF осуществлялся методом РСК (см. п. 2.2), как с учетом однократных и двукратных, так и только однократных кластерных амплитуд. Симметрия задачи учитывалась в рамках группы C2v. Молекулярные орбитали (используемые на стадии РСК) были получены в результате расчета конфигурации A116B16B26A22 методом самосогласованного поля (ССП) со спин-усредненной частью ОРЭПО (см. п. 2.1) в базисе контрактированных орбиталей гауссова типа: [26s,25p,18d,12f,10g/6s,6p,4d,2f,1g] – для атома таллия и [14s,9p,4d,3f/4s,3p,2d,1f] – для атома фтора. Использовался 21-электронный ОРЭПО, моделирующий взаимодействие остова [Kr]4d3/244d5/264f5/264f7/28 с внешними остовными и валентными электронами (запись [Kr] означает электронную конфигурацию криптона).Процедура расчета матричных элементов (3) и (5) описана в п. 2.3 и 2.4.
2.1
Обобщенный Релятивистский Эффективный Потенциал ОстоваМетод ОРЭПО [
4] основан на идее разделения орбитального пространства на три области: внутреннюю остовную, внешнюю остовную (или промежуточную) и валентную. Он позволяет исключить из расчетов внутренние остовные электроны тяжелого атома, смоделировав их взаимодействие с валентными электронами посредством эффективного потенциала. В отличие от других известных из научной литературы методов РЭПО, Обобщенный РЭПО дает возможность сочетать практически любую требуемую точность расчета корреляционной структуры в валентной области с максимально возможной простотой и экономичностью этого расчета. Это в первую очередь касается минимизации атомных базисов и количества двухэлектронных интегралов молекулярного гамильтониана. Кроме того, он позволяет наиболее простым образом учесть релятивистские эффекты, которые могут быть весьма существенны для корректного расчета молекул с тяжелыми элементами. В частности, можно исключить из расчета малые компоненты дираковских спиноров. ОРЭПО в спинорном представлении записывается следующим образом:![]()
![]()
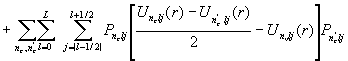 , (6)
, (6)
где
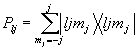
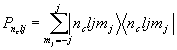
L – величина, которая на единицу больше максимального орбитального момента внутренних остовных орбиталей, J = L+1/2.
Оператор ОРЭПО можно переписать в спин-орбитальном представлении. При этом оператор ОРЭПО будет являться суммой Усредненного Релятивистского Эффективного Потенциала, который учитывает независящие от спина релятивистские эффекты, и Эффективного Спин-Орбитального Потенциала.
Молекулярные псевдоорбитали в методе ОРЭПО являются двухкомпонентными, они правильно описывают поведение волновой функции в валентной области, но сглажены в области ядра атома таллия, поэтому они не пригодны для расчета матричных элементов операторов, сингулярных в области ядра. Кроме того, в этой области нельзя пренебрегать и малыми компонентами. Поэтому для расчета параметров
Молекула TlF в основном состоянии хорошо описывается методом релятивистских связанных кластеров РСК для закрытых оболочек. Метод РСК для закрытых оболочек является наиболее простым и одновременно наиболее исследованным вариантом РСК. В этом методе волновая функция записывается в виде:
![]() , (7)
, (7)
где
![]() , (8)
, (8)
индексы
Для отыскания коэффициентов
![]() , (9)
, (9)
где
Полная энергия задается выражением:
![]() (10)
(10)
Мы использовали вариант метода РСК с однократными и двукратными кластерными амплитудами:
Для сравнения с результатами, полученными в других работах методом Хартри-Фока-Дирака, мы провели соответствующие расчеты с учетом только однократных возбуждений:
Однако исходное состояние
Для расчета среднего значения оператора ![]() на кластерной волновой функции необходимо вычислить выражение:
на кластерной волновой функции необходимо вычислить выражение:
![]() , (11)
, (11)
где символ С означает, что учитываются только связанные диаграммы.
Член
![]() , (12)
, (12)
где
![]() . (13)
. (13)
Для практического использования формулы (12) проводился расчет с гамильтонианом молекулы TlF и расчет, в котором вместо гамильтониана использовался оператор (13). В этом случае:
![]() , (14)
, (14)
где
В таблице 2 приводится значения интеграла (14), рассчитанное для разных значений
![]() , (15)
, (15)
где
Из таблицы 2 видно, что при использовании формулы (15) необходимый уровень точности достигается при большем значении
![]() . (16)
. (16)
2.4 Восстановление волновой функции в области атомного ядра, расчет величин
Для восстановления волновой функции в области ядра мы использовали процедуру невариационного восстановления
[5], которая основана на построении эквивалентных четырехкомпонентных базисных наборов:![]() , (*)
, (*)
где
и двухкомпонентных:
![]() (**)
(**)
базисных наборов. Эквивалентные спиноры
Для атомной орбитали
![]() . (17)
. (17)
Можно показать, что если ограничиться рассмотрением первых возбужденных состояний, то разложение соответствующего четырехкомпонентного молекулярного спинора
![]() . (18)
. (18)
Таким образом, восстановленная молекулярная орбиталь определяется линейной комбинацией (18), коэффициенты разложения которой определяются из уравнения (17).
Для разложения двухцентровой молекулярной орбитали, полученной из ОРЭПО расчета по набору (**), который центрирован на атоме таллия мы использовали ее одноцентровое представление:
![]() , (19)
, (19)
где
Как уже говорилось, параметры
Как следует из (16), значения параметров
Проведенный нами расчет величины
Ограничившись в разложении (19) учетом только s и p функций, Parpia
[7] (при расстоянии R=2,0844 Å) получил значениеРасчет параметра
Таблица 1
|
Расстояние Å |
2.0844 |
2.1 |
|||||||||
|
Разложение |
s,p |
s,p,d |
s,p,d,f |
s,p |
s,p |
s,p,d,f |
s,p |
||||
|
Неприво-димое предста- вление |
№ |
|
|
|
|
||||||
|
A1 |
1 |
0.00 |
0.01 |
0.01 |
1.7 |
0.00 |
0.01 |
0.5 |
|||
|
2 |
-1.23 |
-1.23 |
-1.23 |
-552.3 |
-1.21 |
-1.21 |
-540.3 |
||||
|
3 |
2.09 |
1.95 |
1.95 |
943.2 |
2.04 |
1.90 |
920.5 |
||||
|
4 |
-0.39 |
-0.32 |
-0.32 |
-179.3 |
-0.37 |
-0.30 |
-168.1 |
||||
|
5 |
0.00 |
0.00 |
0.00 |
0.0 |
0.00 |
0.00 |
0.0 |
||||
|
6 |
0.00 |
-0.02 |
-0.03 |
-1.0 |
0.00 |
-0.03 |
-1.2 |
||||
|
7 |
-4.70 |
-5.03 |
-5.04 |
-2209.5 |
-4.70 |
-5.02 |
-2213.0 |
||||
|
8 |
14.09 |
13.62 |
13.62 |
6487.8 |
14.01 |
13.56 |
6456.8 |
||||
|
B1 |
1 |
0.00 |
-0.06 |
-0.06 |
0.0 |
0.00 |
-0.06 |
0.0 |
|||
|
2 |
0.00 |
0.08 |
0.07 |
0.0 |
0.00 |
0.07 |
0.0 |
||||
|
3 |
0.00 |
-0.10 |
-0.10 |
0.0 |
0.00 |
-0.09 |
0.0 |
||||
|
B2 |
1 |
0.00 |
-0.06 |
-0.06 |
0.0 |
0.00 |
-0.06 |
0.0 |
|||
|
2 |
0.00 |
0.08 |
0.07 |
0.0 |
0.00 |
0.07 |
0.0 |
||||
|
3 |
0.00 |
-0.10 |
-0.10 |
0.0 |
0.00 |
-0.09 |
0.0 |
||||
|
A2 |
1 |
0.00 |
0.00 |
0.00 |
0.0 |
0.00 |
0.00 |
0.0 |
|||
|
Сумма |
19.72 |
17.64 |
17.56 |
8981.2 |
19.54 |
17.45 |
8910.4 |
||||
|
|
- |
- |
- |
9604.9 |
- |
- |
|||||
|
|
- |
16.21 |
14.15 |
- |
|||||||
Таблица 2. Значения выражений (14) и (15) полученные при расчете
|
|
1*10-4 |
-1*10-4 |
1*10-5 |
-1*10-5 |
1*10-6 |
-1*10-6 |
|
Формула (14) |
-9.28 |
2.66 |
-3.92 |
-2.72 |
-3.42 |
-3.23 |
|
Формула (15) |
3.31 |
3.32 |
3.325 |
|||
Таблица 3.
Значения параметров X и M полученные в настоящей и других работах.|
Работа |
Данная работа |
[6] |
[7] |
|
|
Точка расчета, Å |
2.0844 |
2.1 |
2.0844 |
2.1 |
|
Способ расчета |
РСК-О |
Хартри-Фок-Дирак |
Хартри-Фок-Дирак |
|
|
|
9604.9 |
7743 |
8747 |
|
|
|
14.15 |
15.61 |
13.63 |
|
Список литературы
1. M. G. Kozlov and L. N. Labzowsky “ Parity violation effects in diatomics” J.Phys.B, V.28
1933-1961 (1995).
2. L. I. Schiff “Measurability of Nuclear Electric Dipole Moments” Phys.Rev., V. 132 , 2194-
2200 (1963);
3. Hinds E.A. and Sandars P.G.H. "Electric dipole hyperfine structure of TlF" Phys. Rev. A,
4. Titov A.V. and Mosyagin N.S. "Generalized Relativistic Effective Core Potential:
Theoretical grounds." Int.J.Quant.Chem., V. 71, p. 359-401,1999;
A.V.Titov and N.S.Mosyagin, ``Generalized Relativistic Effective Core Potential Method:
Theory and Calculations'' Rus.J.Phys.Chem., V.74, Suppl. 2, p. 376-387, 2000.
5. Titov A.V. "A Two-step Method of Calculation of Electronic Structure of Molecules with
Heavy Atoms. Theoretical Aspect." Int.J.Quant.Chem., V. 57, p. 453-463, 1996;
A.V.Titov, N.S.Mosyagin, and V.F.Ezhov "P,T-Odd Spin-Rotational Hamiltonian for YbF
Molecule" Phys.Rev.Lett., V.77, p. 5346-5349 (1996);
M.G.Kozlov, A.V.Titov, N.S.Mosyagin, and P.V.Souchko, ``Enhancement of the electric
dipole moment of the electron in BaF molecule'', Phys.Rev.A, V.56(5), R3326-R3329
(1997);
N.S.Mosyagin, M.G.Kozlov, and A.V.Titov, ``Electric dipole moment of the electron in
the YbF molecule'', J.Phys.B, V.31 L763-L767 (1998).
6. Parpia F.A. "Electric-dipole hyperfine matrix elements of the ground state of the TlF
Molecule in the Dirac-Fock approximation" J. Phys. B, V. 30, p. 3983-4001, 1997.
7. Quiney H.M., Laerdahl J.K., Faegri K., Jr., and T. Saue "Ab initio Dirac- Hartree-Fock
calculations of chemical properties and PT-odd effects in thallium fluoride" Phys. Rev.
A, V. 57, p. 920-944, 1998